 Home page
Home page Home page Home page |
Backgammon home page |
Usage : The first section sets the essentials of the whole article. Every of the three next sections is then standalone and can be skipped without damaging understanding.
A pattern caught your attention while you were reading your local newspaper. First of all, you went to the report of yesterday's football, in which Blue beat Red by 1-0 in a rather lucky way. Red played fine but didn't manage to score, hitting the bar three times instead. On the other hand, Blue produced almost no play but was awarded a very controversial penalty by the referee. Although the journalist objectively acknowledges Blue's sheer good luck, he also seems to put high praise on its trainer for his tactical choice of going all for the defense; on the other hand, Red's trainer is criticized for having selected the attacker who happened to be involved in all of Red's three near misses. But hadn't the journalist told beforehand that Red had deserved the win?
Well, one doesn't need to be the brightest light of the bulb in order to become a sport columnist, or so you think while turning to the local column, which features the trial of a drunk driver who has killed a kid on a pedestrian crossing. You rejoice at first about the two-year imprisonment sentence and the new-found severity in dealing with irresponsible driving. But you are then reminded of a case one year ago, when another drunk driver nearly missed a similar accident because a passerby saw it coming and managed to push the kid aside at the last second. That driver only had his driving license suspended for six months. Aren't you beginning to ask yourself whether there isn't something fishy in the way we assess our own acts after their consequences have been revealed?
The answer is, there is something fishy about it indeed, fishy enough for having been labelled outcome bias by psychologists. The outcome bias is the tendency to "judge a past decision by its ultimate outcome instead of based on the quality of the decision at the time it was made, given what was known at that time" [6]. As your newspaper showcased, that bias is extremely common, and does indeed deeply affect our ethical judgements and our legal system. [1]
The clearest way to debunk the outcome bias is with the help of games that mix skill and chance. Besides being fun, those are probably the best available mind tools for rational choice, since they set players in a form of competition for rationality.
Backgammon will be my game of choice. For understanding the examples you will need to know only the basic rules of checker movement, and the usage of the doubling cube. This page does a pretty good job at explaining those ("Movement of the Checkers", rules 1-3, "Doubling", paragraph 1-2).
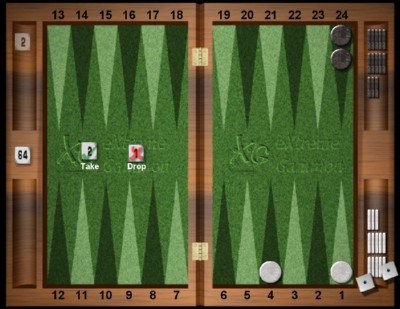
Here is the last roll in a $10 money game, both sides being almost done driving their checkers home (they end their race at the right of the board). As White you are a huge favourite since you will win unless you roll very small, e.g. a 2-1. Seeing that, you offer the doubling cube to Bigfish. Then a classical scenario occurs: Bigfish accepts the cube, you tell him that he should have declined and lost only $10, you roll 2-1 and curse, he wins $20 and he tells you the infamous "See, I was right to accept".
Outcome bias, you think1, but what can you do about it? After all, it is not obvious that Bigfish really made a mistake; sure he was a underdog to win the game, but on the other hand, compared with the alternative of giving up $10, losing $20 instead is not as bad as winning $20 would be sweet. In order to find out what the rational decision would have been, we will need a simple probabilistic computation.
First of all, out of 36 rolls there are 7 rolls that fail to win the game : 1-1, 2-1, 1-2, 3-1, 1-3, 3-2 and 2-3 (2-2 is fine since four twos can be played). When Bigfish accepts the cube, he will win $20 if you roll one of those, and lose $20 if you roll any of the 29 other rolls. Suppose that you play that position 36 times and that Bigfish accepts the cube every time. On average he will win $140 (7*20) and lose $580 (29*20); he will end up $440 poorer. On the other hand, if Bigfish declines the cube every time, he will lose only $360 (36*10). That is why accepting the cube was indeed a poor decision. One can even quantify how poor: accepting the cube costs exactly $80 / 36 = $2.22!
You might protest that making the above mistake is not "exactly" the same as losing $2.22. Nevertheless, how similar it is follows from the law of large numbers [5], which in a nutshell states that luck always almost cancels out in the long run. So while the present decision may not cost Bigfish $2.22 (indeed it hasn't!), if you play him long enough, you will win a lot of money if he continues to make such errors (and if you don't!).
The above example was meant to shatter two common fallacies: "I was right because I won" and "It doesn't matter since luck will be deciding it anyway". It should also clarify how professional players manage to make money so consistently in games like backgammon. One reason why they make more money than lesser players is that they have learned to compute rather than relying on outcomes only.
Building on numerous monetary examples similar to our backgammonish one, die-hard economists suggest that we should rate every decision by discarding outcomes completely and by computing mathematical expectancies like we did above.
But have we really raised so high above our biological evolution? On the other hand, die-hard evolutionary psychologists argue the bias label has often be sticked too hastily, and that it might be only cultural norms that depicts us as acting against our actual interests. Since our psychology has been shaped by natural selection, which shows a tremendous record of being smarter than we are, telling that we know better could be a sin of vanity.
One more concrete objection is that the structure of the real world tends to be less stable and predictable than the experimental settings. Another objection is against the general requirement for experimental subjects to dismiss irrelevant factors (e.g. the likely social status of the experimenter), although in real life these factors can easily be relevant. In the concise words of Steven Pinker, "outside of school, of course, it never makes sense to ignore what you know" [3].
Can such objections apply to the outcome bias? Definitely! The first point is that reality might not always be what you think it is. For instance, people who discard outcomes completely would never suspect a cheater who performs a little too well to be honest. And what about social factors? In all societies, people who have enjoyed a lot of good outcomes tend to move towards the high end of the power scale, and it might be an adaptive strategy to have might make right. Maybe flattering winners is just erring on the side of caution.
Nevertheless, Pinker's nice aphorism is factually wrong. Not only in backgammon are there countless cases when it makes sense to ignore something you know. For instance, when a merchant is trying to sell you a very expensive car, it makes perfect sense for you to ignore the social cues given by his likeable behavior, which suggest a reciprocity that is definitely not called for.
As for the outcome bias, it can't be only a good thing. Consider the classic story of a trader (or entrepreneur) who has quickly (and luckily) become rich. If he concludes that making money is easy, he is at a high risk of losing everything again with recklessly optimistic actions. Surely that must be maladaptive even in the strictest biological sense.
The bottom line is that neither the die-hard economist nor the die-hard evolutionary psychologist is right (for a more in-depth discussion, see [4]). Actually, the last section will show that a subtler form of outcome bias could be hidden behind the tendency of scientific minds confronted to such questions to gravitate towards one of the two extreme solutions, even when the correct answer lies somewhere inbetween...
The conclusion of the previous section might be a bit disappointing, since we haven't learnt much about how to overcome the outcome bias without becoming outcome-blind. The uplifting message of the present section will be that there exist ways of keeping the best of the two worlds. One of them is called variance reduction and will again be exemplified by backgammon.
Don't go straight to Wikipedia and be put off by the barbaric formulae of variance reduction for statisticians. The root concept is actually rather simple. The idea is to start with the actual outcome, but to mitigate it with every factor that we can identify as pure luck2. When applied correctly, that idea has the virtue of shortening "the long run", and can give reliable results from a much smaller sample of trials.
In backgammon, variance reduction has been successfully applied to the computer simulations that are currently the best way of assessing a particular position (starting from the given position, the program plays a ton of games against itself and records the results). According to expert David Montgomery, using variance reduction in such simulations makes each game worth about twenty-five games information-wise [2].
But that stuff is for computer nerds, do you think. Not necessarily! Here is how the idea of variance reduction can be applied "by hand" in a backgammon game by a clever player.

In the above position you have White and quite a nice blockade against Lesserfish's lonely back checker. If you manage to extend that block to six consecutive points, the checker will be definitively trapped and the game will be almost won. So all you need is to add the point labelled "10" to your blockade, task on which you can work in relative safety.
You offer the doubling cube, and Lesserfish accepts it much to your surprise. By virtue of a computation similar to our first example (but omitting some subtleties), she needed about 25% of winning chances in order to correctly accept your cube; it seems clear to you that she will win far from that often. You then proceed to win the game, which would very much confirm your initial assessment if you were prone to the outcome bias.
But during the course of the game, you have been attentive enough to notice some turns where your opponent had one or more escaping rolls, when you were slightly lucky that she didn't roll them. For instance, on his first roll Lesserfish could already escape your blockade with a 6-1 or 1-6 (5,5% of chances) after which she would have been a slight favourite to find her way home and win outright (say 3% of won games). The same happened one move later. Then some moves later, she could escape with a 6 (30% of escaping chances, about 20% of immediate wins). That means that in the course of the game, you have been lucky for an amount of about 26%, making 29% if we add 3% of remaining chances for Lesserfish after you have completed your blockade. In the other dice rolls you didn't notice anything especially lucky or unlucky.
So your quick and dirty variance reduction corrects your result (100% since you won) by 29%, telling that luck set apart you won only "71% of a game" (that sounds absurd, but such is your variance reduced outcome). Now Lesserfish's decision doesn't seem so unlikely to be correct after all. And indeed, a computer simulation (with variance reduction, of course!) shows that she had as many as 27% of winning chances, making her right for accepting your doubling cube!
Naturally the above example is contrived and the one-game approximation will generally not be that precise. But in view of the likely future reoccurrences of such a position, you would be much better off if you intuitively learned to register variance reduced outcomes into your mental database, rather than actual outcomes.
For a final twist, let me show in a (hopefully) somewhat original setting how sticky the outcome bias can be when it comes in disguise, even to someone well aware of it, and who should really know better (me). Here is a personal experience with the Swiss health care system, tweaked for simplicity in a way that preserves the cognitive illusion.
Every year, like every Swiss people I had to choose between the three following variants.
For instance, with variant 2 and $1500 of medical expense, my insurance would cover only the last $500 of those $1500. So my yearly cost would be $1000 plus $400 (the premium, that I have to pay in any case), for a grand total of $1400.
The system looked simple enough for me to approach it the economist's way. I drew the following graphic in order to express my yearly cost in function of my medical expense, for each of the three variants.
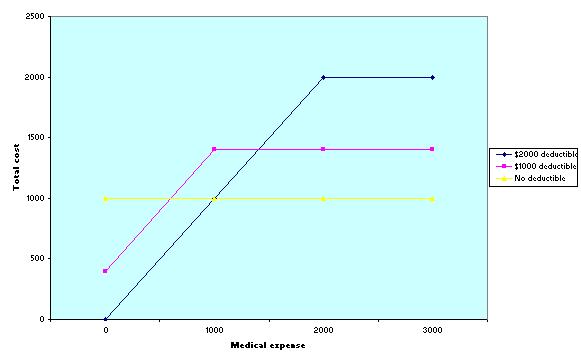
A quick look at the graphic told me that whatever my medical expense, the variant 2 (purple line) could never be the best choice. For high medical expense, the variant 1 (yellow line) fared better, while for low medical expense, the variant 3 (black line) was the way to go. For intermediate medical expenses such as $1000, the variant 2 was even the worst of the three. That made clear that only a sucker would choose variant 2. The rational solution was to figure out my expected medical expense, and to choose variant 1 or 3, depending on whether that expected expense was below or over $1000. Elementary, my dear Watson?
In fact, though tempting it was, and though I have since read the exact same advice in two different magazine articles, the above reasoning was dead wrong, as I realized later and as can be shown by introducing an explicit uncertainty into the medical expense.
Suppose that you hate doctors and drugs, but that due to some condition you sometimes get a serious seizure, for which you must be urgently hospitalized. Every year there is approximatively a 50% chance that you get a seizure and have $2000 of medical expense, otherwise you will have zero medical expense. Let us see what you can expect to pay in each variant.
Surprise, in that case the deductible for suckers is your best bargain!3 Let us unfold my "rational" line of thought again in order to understand where it went wrong. At first, I have circumvented the outcome bias by making sure to consider all possibilities of medical expense. But after having drawn the graphic, I did as if I could know my medical expense after all. In doing so, I managed to commit the outcome fallacy on a hypothetical outcome!
The above example may seem artificial because it arises from a set of arbitrary rules. But the exact same trap can kick in when considering yet to be validated scientific theories. Suppose that you have three competing scientific theories A, B and C that await a common experimental test, which unfortunately requires a more advanced technology than we presently have. If the result of the test comes "true", then A is more likely than B, which is more likely than C. If the result of the test comes "false", then C is more likely than B, which is more likely than A.
When thinking about which theory might be the best one, most scientists are likely to gravitate towards one of the extremes A and C and consider B as an inferior theory, even though the considered experiment is not done. But as our insurance policy computation has shown, it is a very real possibility than in the state of our present knowledge, B is indeed the most likely theory!
[1] Gino, F., Moore, D.A., Bazermann, M.H., No harm, no foul: The outcome bias in ethical judgments, Harvard Business School, 2008 [2] Montgomery, David, Variance Reduction, http://www.bkgm.com/articles/GOL/Feb00/var.htm [3] Pinker, Steven, How the Mind Works, Norton, 1997 [4] Stanovich, Keith, The Robot's Rebellion, University of Chicago Press, 2004 [5] Wikipedia, The law of large numbers, http://en.wikipedia.org/wiki/Law_of_large_numbers [6] Wikipedia, Outcome bias, http://en.wikipedia.org/wiki/Outcome_bias